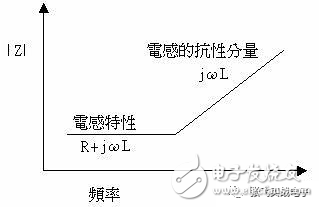
Traditionally, EMC has always been seen as "black magic." In fact, EMC can be understood by mathematical formulas. However, even though mathematical analysis methods are available, those mathematical equations are still too complex for actual EMC circuit design. Fortunately, in most practical work, engineers do not need to fully understand the complex mathematical formulas and the theoretical basis that exists in the EMC specification. Just by using a simple mathematical model, you can understand how to meet EMC requirements. . Wires, traces, mounts, etc., which are seemingly inconspicuous components, often become the best emitter of RF energy (ie, the source of EMI). Each component has an inductance, which includes the bond wire of the silicon wafer, and the pins of the resistor, capacitor, and inductor. Each wire or trace contains hidden parasitic capacitance and inductance. These parasitic elements affect the impedance of the wire and are sensitive to frequency. Depending on the value of LC (determining the self-resonant frequency) and the length of the PCB trace, self-resonance can be generated between a component and the PCB trace, thus forming an efficient radiating antenna. At low frequencies, the wire has only a characteristic of resistance. However, at high frequencies, the wires have the characteristic of inductance. Because it becomes a high frequency, it will cause changes in the impedance, and thus change the EMC design between the wire or PCB trace and ground. It is necessary to use the ground plane and the ground grid. The main difference between a wire and a PCB trace is that the wire is round and the wire is rectangular. The impedance of the wire or trace includes the resistance R and the inductive reactance XL = 2πfL. At high frequencies, this impedance is defined as Z = R + j XL j2πfL, and no capacitive reactance Xc = 1/2πfC is present. When the frequency is higher than 100 kHz, the inductive reactance is greater than the resistance. At this time, the wire or the trace is no longer a low-resistance connecting wire, but an inductance. In general, wires or traces that work above the audio should be considered as inductors and can no longer be viewed as resistors, but can also be RF antennas. The length of most antennas is equal to 1/4 or 1/2 wavelength (λ) of a particular frequency. Therefore, in the EMC specification, wires or traces are not allowed to operate below λ/20 of a particular frequency, as this will suddenly turn it into a high-performance antenna. Inductors and capacitors can cause resonance in the circuit. This phenomenon is not documented in their specifications. For example: Suppose there is a 10 cm trace, R = 57 mΩ, 8 nH/cm, so the total inductance is 80 nH. At 100 kHz, an inductive 50 mΩ is obtained. When the frequency exceeds 100 kHz, this trace will become an inductor and its resistance is negligible. Therefore, this 10 cm trace will form an efficient radiating antenna at frequencies above 150 MHz. Since the wavelength λ = 2 meters at 150 MHz, λ/20 = 10 cm = the length of the trace; if the frequency is greater than 150 MHz, its wavelength λ will become smaller, and its 1/4 λ or 1/2 λ value will Close to the length of the trace (10 cm), it gradually formed a perfect antenna. Resistance is the most common component on a PCB. The material of the resistor (carbon synthesis, carbon film, mica, winding type, etc.) limits the effect of frequency response and the effect of EMC. Wirewound resistors are not suitable for high frequency applications because of the excessive inductance present in the wires. Although the carbon film resistor contains an inductor, it is sometimes suitable for high frequency applications because its pin has a small inductance value. What is often overlooked is the package size and parasitic capacitance of the resistor. Parasitic capacitance exists between the two terminals of the resistor, and at very high frequencies, it can damage normal circuit characteristics, especially when the frequency reaches GHz. However, for most application circuits, the parasitic capacitance between the resistor pins is not as important as the pin inductance. When the resistance is subjected to an overvoltage stress test, attention must be paid to the change in resistance. If an "electrostatic discharge (ESD)" occurs on the resistor, something interesting happens. If the resistor is a surface mount component, this resistor is likely to be broken by the arc. If the resistor has a pin, the ESD will find the high resistance (and high inductance) path of the resistor and avoid entering the circuit protected by this resistor. In fact, the true protector is the inductance and capacitance characteristics hidden by this resistor. Capacitors are typically used in power buses to provide decoupled, bypassed, and maintain fixed DC voltage and bulk. A true simple capacitor maintains its capacitance until it reaches its self-resonant frequency. Beyond this self-resonant frequency, the capacitance characteristics will become the same as the imaging inductance. This can be illustrated by the formula: Xc = 1/2 πfC, where Xc is the capacitive reactance (unit is Ω). For example, a 10μf electrolytic capacitor has a capacitive reactance of 1.6Ω at 10 kHz and 160μΩ at 100 MHz. Therefore, at 100 MHz, there is a short circuit effect, which is ideal for EMC. However, the electrical parameters of the electrolytic capacitor: equivalent series inductance (ESL) and equivalent series resistance (ESR) will limit this capacitor to operate at frequencies below 1 MHz. The use of capacitors is also related to the pin inductance and volume structure. These factors determine the number and size of parasitic inductance. Parasitic inductances exist between the bonding wires of the capacitors. They cause the capacitor to behave like an inductor when it exceeds the self-resonant frequency, and the capacitor loses its previously set function. The inductor is used to control EMI within the PCB. For an inductor, its inductive reactance is proportional to the frequency. This can be illustrated by the formula: XL = 2πfL, which is the inductive reactance (in Ω). For example: an ideal 10 mH inductor with an inductive reactance of 628 Ω at 10 kHz and 6.2 MΩ at 100 MHz. So at 100 MHz, this inductor can be considered an open circuit. At 100 MHz, passing a signal through this inductor will cause a drop in the quality of this signal (this is observed from the time domain). Like capacitors, the electrical parameters of this inductor (parasitic capacitance between coils) limit the ability of this inductor to operate below 1 MHz. The problem is, if you can't use the inductor at high frequencies, what should you use? The answer is that you should use "ferrite bead". The iron powder material is iron-magnesium or iron-nickel alloy. These materials have high permeability. At high frequency and high impedance, the capacitance between the coils inside the inductor will be the smallest. Iron powder beads are usually only suitable for high-frequency circuits, because at low frequencies, they basically retain the complete characteristics of the inductor (including resistance and resistance components), thus causing slight losses on the line. At high frequencies, it basically only has a resistance component (jωL), and the resistance component increases as the frequency increases, as shown in Figure 1. In fact, iron powder beads are high frequency attenuators for RF energy. In fact, iron powder beads can be considered as a resistor in parallel with an inductor. At low frequencies, the resistor is "short-circuited" by the inductor and current flows to the inductor; at high frequencies, the high inductance of the inductor forces current to flow to the resistor. In essence, iron powder beads are a "dissipative device" that converts high-frequency energy into heat. Therefore, in terms of performance, it can only be interpreted as a resistor, not an inductor. The transformer is usually present in the power supply. In addition, it can be used to insulate the data signal, I/O connection, and power supply interface. Depending on the type and application of the transformer, there may be a shield between the primary and secondary coils. This shield is connected to a grounded reference source to prevent capacitive coupling between the two sets of coils. Transformers are also widely used to provide common mode (CM) insulation. These devices magnetically couple the primary side coil and the secondary side coil to deliver energy based on a differential mode (DM) signal through its input. As a result, the CM voltage passing through the primary side coil is rejected, so that the common mode insulation is achieved. However, when manufacturing the transformer, there is a signal source capacitance between the primary side and the secondary side coil. As the circuit frequency increases, the capacitive coupling capability also increases, thus damaging the insulation of the circuit. If there is enough parasitic capacitance, high-frequency RF energy (from fast transients, ESD, lightning strikes, etc.) may pass through the transformer, causing the circuit at the other end of the insulation layer to also receive this momentary change. Voltage or high current. The hidden features of various passive components have been described in detail above, and the underlying explanations of why these hidden features can cause EMI in the PCB. The passive components described above have hidden features and generate RF energy in the PCB, but why? In order to understand the reason, you must understand the Maxwell equation. Maxwell's four equations illustrate the relationship between electric and magnetic fields, and they are derived from Ampere's law, Faraday's law, and Gauss's law. These equations describe the characteristics of electromagnetic field strength and current density in a closed loop environment and need to be calculated using higher calculus. Because the Maxwell equation is very complex, it is only briefly explained here. In fact, PCB wiring engineers do not need to fully understand the detailed knowledge of Maxwell's equations, as long as they understand the key points, they can complete the EMC design. The complete Maxwell equation is listed below: The first law: electric flux (from Gauss' law) The second law: magnetic flux (from Gauss' law) The third law: electric potential (from Faraday's law) The fourth law: electric current (from Ampere's law) In the above equation, J, E, B, and H are vectors. In addition, the basic physical concepts associated with the Maxwell equation are: The Maxwell equation illustrates the interaction between charge, current, magnetic field, and electric field. ◠"Lorentz force" can be used to describe the physical forces exerted by electric and magnetic fields on charged particles. ◠All substances have a compositional relationship with other substances. This includes: 1. Conductivity: The relationship between current and electric field (Ohm's law of matter): J = σE. 2. Magnetic permeability: the relationship between magnetic flux and magnetic field: B = μH. 3. Dielectric constant: The relationship between charge storage and an electric field: D = εE. J = conducted current density, A/m2 σ= conductivity of the substance, E = electric field strength, V/m D = flux density, coulombs/ m2 ε = vacuum permittivity (permittivity), 8.85 pF/m B = magnetic flux density, Weber/ m2 or Tesla H = magnetic field, A/m μ= permeability coefficient of medium, H/m According to Gauss's law, Maxwell's first equation is also called "divergence theorem". It can be used to illustrate the electrostatic field E produced due to the accumulation of charge. This phenomenon is best observed between two boundaries: conductive and non-conductive. According to Gauss's law, the behavior under boundary conditions produces a conductive cage (also known as a Faraday cage) that acts as a static shield. In an enclosed area surrounded by a Faraday box, electromagnetic waves around the outside are inaccessible to this area. If an electric field is present in the Faraday box, at its boundary, the charge generated by this electric field is concentrated inside the boundary. The charge outside the boundary is rejected by the internal electric field. Maxwell's second equation states that there is no magnetic charge in nature, only the presence of charge, that is, the absence of a single magnetic pole. Although the current Grand Unified Theory predicts that there are few magnetic charges, it has not been proven by experiments. These charges are positively or negatively charged. The magnetic field is generated by the action of current and electric field. Due to the emission of current and electric fields, they become the source of radiant energy. The magnetic field forms a closed loop around the current, which is generated by the current. Maxwell's third-party program, also known as "Faraday's Law of Induction," shows that when a magnetic field surrounds a closed circuit, the magnetic field causes the closed circuit to generate current. The third-party program and the fourth equation are accompanied. A third-party program indicates that a changing magnetic field produces an electric field. Magnetic fields are usually found in transformers or coils, such as motors, generators, etc. The interaction of the third and fourth equations is the main focus of EMC. Together, they illustrate how the coupled electric and magnetic fields radiate or propagate at the speed of light. This equation also illustrates the concept of "skin effect", which predicts the effectiveness of "magnetic shielding." In addition, it also describes the characteristics of the inductor, and the inductor allows the antenna to exist reasonably. Maxwell's fourth equation is also called Ampere's law. This equation illustrates two sources of magnetic fields. The first source is that the current is flowing in the form of a transport charge. The second source is that when a changing electric field surrounds a closed circuit, a magnetic field is generated. These sources of electricity and magnetism illustrate the effects of inductance and electromagnetics. In this equation, J represents the component of the magnetic field generated by the current; As mentioned earlier, the changing current will generate a magnetic field, and the static charge distribution will generate an electric field. The relationship between the current and the radiated electric field will be further discussed below. We must examine the structure of the current source and see how it affects the radiated signal. In addition, we must also note that the farther away from the current source, the lower the signal strength. Time-varying currents exist in two structures: 1. The source of the magnet (which is a closed loop), 2. The source of the electricity (which is a dipole antenna). First explore the source of magnetism. As with most electronic engineering designs, EMC design requires careful consideration. When reading this article, the reader should also refer to the EMC practice that is usually performed, so that you may find many places that have not been noticed in the past, and these places are often the most vulnerable places for EMI. In an era that emphasizes the rapid launch of products, the pressure on engineers is increasing. Using good EMI simulation tools can help us get things done quickly; but if you rely too much on these tools, you may not be able to do the same in some very special situations or circumstances. Therefore, having a profound theoretical foundation will make up for the shortcomings of the normal practice. Fork Type Connecting Terminals Fork Type Connecting Terminals,Terminals,Connecting Terminals Taixing Longyi Terminals Co.,Ltd. , https://www.longyicopperterminals.com
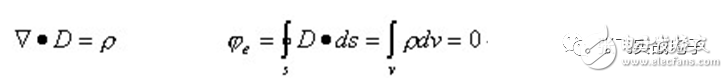
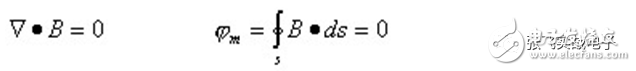
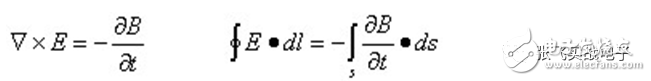
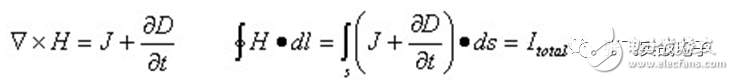
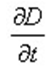 It is the component of the magnetic field generated by the electric field.
It is the component of the magnetic field generated by the electric field. 
What are the hidden features of passive components in EMC design?
introduction